Conference Material

Rubenstein 1999 Keynote Address

Teachers and Science

Scientists and teachers do science very differently,and nowhere is this difference more clearly illustrated than in the classic black box experiment. You know it because you have done it. You get this little box and something will be in it. Your job is to figure out what the something is or how the wires or tubes inside work (Figure 10). And when you get done and have your answer you find out if you are right and if you are, then you stand up and share your reasoning process with others. Up to a point this is science. But when I sit at the table with my science teachers, I reach under the table and grab the answer sheet and tear it up. At the end my group never knows what really was in the box, or how the box's process works. My group has to defend their reasoning process without knowing if they have it right. This is real science. Scientists can't open the box, they never really know what's in the box.

To get around this problem in a workshop like this it would be essential for no one to know what's in the box, and therefore for everyone to stand up and share their reasoning about what they think is in the box. They would have to share their model, their hypothesis and its predictions and then how they tested it. Finally, everybody would have to get together and search for generalizations. By comparing and noting that what's in your box sounds like, or acts, like what's in my box, each teacher would be testing his or her hypothesis and predictions. This is more like what science is. This is what critical collaboration is and is what takes place at scientific meetings. Remember this point. I will return to it at the very end.

This example of the classic box experiment illustrates what's different between science done by scientists and science done by teachers. The investigating process is the same, but the end is different. We need to remove the artificial ending so typical of classroom science. In Figure 11, I've tried to illustrate the differences. If you look at the onager experiment I just talked about, scientists start with a result, an effect, and try to deduce causes by asking ‘why’ questions. They pick and probe by posing 'what if' scenarios. And then, once scientists believe they have explained a pattern because predictions are substantiated, scientists keep asking 'is the answer right?' Scientists will never know if they are right. They are not gods. They can't open the box. Perhaps they wish they could, but they can't. Scientists have to share their reasoned understanding with colleagues and skeptics and convince them that they are right.

What happens in the classroom between students and teachers? Teachers tend - although it's changing with the emphasis on inquiry based science, but they are not there yet - to move from cause to effect (Figure 11). Whenever teachers hear or give lectures, science is presented as a series of causes which have effects. Lectures give students the perceived wisdom; so do textbooks, teachers' guides, and even kits. In the end teachers are left with the tools that they are provided and they will have to work hard if they are to reverse the arrows between cause and effect.

We all must move away from this style of presentation. We are moving away from canned explanations by encouraging inquiry based learning. But we still have to move away from the search for the right answer.

Let's explore some ways to do this.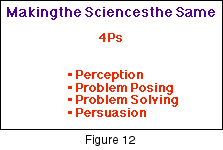 In essence, how can we make science the same between the science that scientists do and the science that students and teachers do in the classroom? We can take the traditional formulation of scientific method and we can change it into what I call the four Ps (Figures 12). We start with perception. This begins by finding a problem that's compelling and creating pattern from apparently chaotic observations. Next we work on problem posing. This means learning to ask a question, which is a guess, or more formally, how to generate a hypothesis? But more important, how do we do so in ways that generates a prediction?

A hypothesis should be of the form that says 'if this, then that'. It shouldn't just be an open-ended question or statement. We wouldn't state that 'temperature is going to affect the process.' A good scientist turns that open-ended statement into one of the form 'when temperature increases such and such will occur.’ We pose a problem by generating a hypothesis with a prediction and then we test whether that prediction is true or false. Performing the test is what we call problem solving.

And then lastly, we spend time persuading others that we are right. Now most of the time we are not going to be right. Someone with a completely different perception of how the world works is going to say, ‘you know, that's crazy, what about this?’ And you realize, 'oh, I didn't think of that.' That's when you are forced to start over. The loop of inquiry goes round and round. It's self-sustaining. It never ends.

This is what scientists do. How then do we teach students how to do this? I use what I call the two E's (Figure 13). I try to engage my students by providing them with compelling issues to be concerned about. And then I try to empower them to act as scientists and solve the problems. One of the courses I teach is introductory biology to non-majors. If you were at Princeton today and you are fulfilling your science laboratory requirement you might take my course! And if you did, you would experience first-hand this process of doing science.

Science and University Students

To illustrate this teaching process I will share with you some experiments that I use to engage and empower students. Each is tied to mathematical concepts, and each is about population dynamics. The students have learned the basic equations that describe change in numbers with respect to time in lecture. But it means little to them. I can show them graphs, I can talk about density dependent or density independent population regulation until I'm blue in the face, and to most of them it will mean little. Unless they manipulate those concepts, they will never create a benchmark experience that will enable them to use ecological reasoning for the rest of their lives. Here is the laboratory exercise as presented to the students.

At the time the laboratory exercise was designed the incipient reintroduction of wolves into Yellowstone Park was just another 'hot button' issue pitting environmental groups against the economic interests of some local residents, in this instance, the ranchers. The exercise was designed to use science to determine if a balanced ecological and economic analysis could be designed that would avert an outcome where bitterness would linger. Hence the title, "The Wolves are Coming. My What Big Teeth They Might Have." Maybe the reintroduction would cause a problem; maybe it wouldn't.

This lab worked for two years. We put a lot of effort into it, but we stopped using it after two years, because we knew the answer. It was no longer a compelling issue. As a teacher, I have to reinvent ways to use my pedagogy to engage students. If the problem isn't fascinating, they'll just do it because I tell them to. I can teach it, but they won't learn it. That's rule number one: if it's not compelling, it doesn't have a chance of being a long lasting learning experience that can serve as a foundation for life-long learning.

In the wolf exercise, students learn concepts. They learn to apply them and learn something about wolves in Yellowstone. The purpose of this lab is to get students to build a complex ecosystem that is dynamically stable before introducing wolves and measuring their impact. They don't know before they start whether they're going to be ecologists hired by the ranchers, or ecologists hired by the National Parks Service. Both have to simulate the same process. In the end they will represent their clients and argue their cases before me and other environmental commissioners and try to convince us that we should or should not authorize the release of wolves. If wolves are to be released, how many should be released? If not, why not? They can only put together a coherent plan if they have mastered the material. And that's the whole point of a truly 'hands-on, minds-on' exercise. In the end, some groups go for the jugular and argue their point until the end. Others see the merits of their adversaries and choose to work together to build a consensus.

Because of the way I structure the exercise, after they have a week to play with the models, they come in and present their cases. They get up on their soapboxes and use rhetoric, logic, and data to make their points and they have a great time. Each side gets 20 minutes to make its case. Then they each get ten minutes to cross-examine each other. And then we pause. The commissioners leave the room and the students get half an hour to adjust their models to account for the criticisms that they perceive might destroy their case. When we return, we ask the students if they want to continue the debate or if they want to join forces to build a consensus. About half the time they say 'we think our position's right, those guys are totally wrong,' and they go all out to prove their points. The group that wins the debate gets an A and the group that loses the debate may or may not get an A, depending on the strength of their argument.

At other times the two groups come to some sort of working consensus where the different stakeholders agree. I can never predict how it’s going to work. I set only a few guidelines for them and give them a computer program from ‘Bioquest’ which is a spatially explicit population dynamic model whereby they make an ecosystem (Figure 17 & 18).

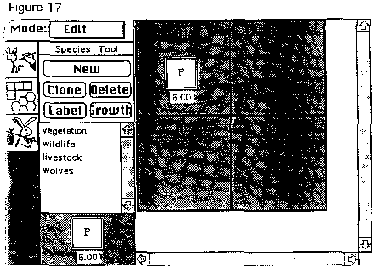
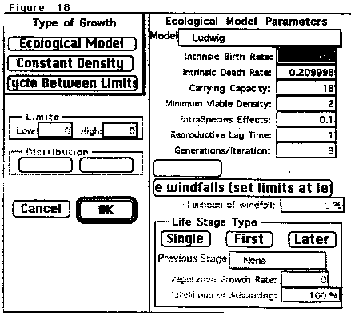
Initially they break the Yellowstone ecosystem down into four areas; three are inside the park where only wildlife can roam and, one is outside the park where wildlife and cattle can live. Students begin by adding vegetation, then wildlife, then livestock and eventually wolves to various areas. But first they have to stabilize each trophic level before adding wolves. And that is not that easy to do. They have to go to the literature and find out the critical life history parameters that shape the demography and the population dynamics of each species at each trophic level. In addition, they have to determine the nature and strength of all pair-wise species interactions before they can run the model.

Figure 19 depicts an example of one of the runs with and without wolves.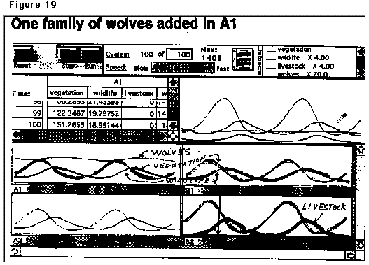 Clearly, at these initial densities wolves don't destabilize the environment and they remain inside the park for 100 years. Notice in the cattle areas though, there's no wildlife. The cattle out-compete the wildlife and generate population cycles that are severe. By running various simulations, students learn many subtle features about the dynamics of populations. Measuring the economic impact of wolves on the cattle complicates the analysis even more. When livestock numbers naturally fluctuate, students have to wrestle with how the impact of wolves is to be determined. At the trough or the top of a cycle? Moreover, in the long run, they have to determine if the presence of wolves will impact the stability of the population? These are the issues students start to learn to tackle when they start to look at the dynamics of the problem. It becomes a very rich learning experience.

Unfortunately, the project burned itself out. So I created another project. It's entitled, "Where Have All the Species Gone? On Bringing Them Back by Managing Population Dynamics". Again, students use computer simulations to learn about the natural dynamics of populations and then how human actions impact those populations. Figure 20 shows what the students begin with: a rationale and a description of the type of analyses they should think about. It’s all very basic and it’s certainly not a cookbook.

In between what you see is a hard core dose of mathematics. Figure 21 shows the shape of the population projection matrix that underlies the computations. It’s basic linear algebra and when coupled to some random process, it forms the core of the model. It projects the size of the population in certain age classes--infants, juveniles, and adults--as a function of the number of infants, juveniles, adults found in the year before. These projection functions are shaped by density and although the mathematics are very straightforward, they account for demographic and environmental variation.

In addition, I give students life tables (age-specific survival and fecundity schedules) of six endangered species. To learn more about each species’ biology (woodpeckers, manatees, dolphins, desert tortoises, wild horses and elephants), they have to go to the literature or use the Web. They get data to characterize these critical parameters in the projection model. In doing so, they have to make some estimates and assumptions because the density dependent relationships for their species have not always been worked out. The students enter the real world of imperfect information, a world where there is not enough time to get it.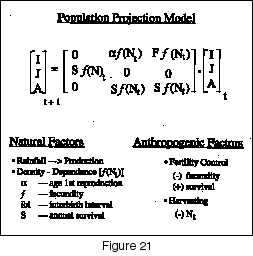

Once they input their data, they generate graphs which they can use to compare different ‘what-if’ scenarios. After a half-hour presentation to the class on how their species would behave in a pristine world, they assess what humans have done to alter their species’ normal behavior. Most importantly at the end they must recommend biologically as well as what practically can be done to rectify the problem. This last feature ties the problem to the real world by forcing students to think about what constraints politics and economics impose on reasonable biological solutions. As you can see both exercises let students explore a compelling problem but force them to engage in ‘if-then’ processing.